Florida’s B.E.S.T 5th Grade Standards
Success in and completion of 5th Grade Math may be determined by a student’s understanding of the 36 standards listed below as well as their ability to answer questions relevant to those standards.
Number Sense and Operations | Fractions
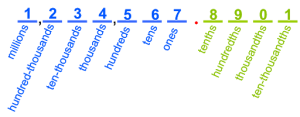 MA.5.NSO.1.1 – Place Value Less Than Zero
MA.5.NSO.1.1 – Place Value Less Than Zero
Express how the value of a digit in a multi-digit number with decimals to the thousandths changes if the digit moves one or more places to the left or right.
When I look at a multi-digit number, I can correctly identify the value of each digit, as high as the millions place and as low as the thousandths place.
- In the number 2,937,057.042, the 9 is in which place value?
- In the number above, the 4 is in which place value?
- Between 8,417,854 and 8,415,855, which two place values are different?
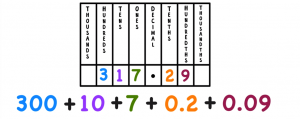 MA.5.NSO.1.2 – Place Value in Different Forms
MA.5.NSO.1.2 – Place Value in Different Forms
Read and write multi-digit numbers with decimals to the thousandths using standard form, word form and expanded form.
I understand that multi-digit numbers can be expressed in three forms and I can write these numbers in three different ways.
- Write the number 2,937,057 in word form.
- Write the number above in expanded form.
- Express the number One million, two-hundred thirty-three thousand, twenty-four and one tenth in standard form.
 MA.5.NSO.1.3 – Place Value Flexibility
MA.5.NSO.1.3 – Place Value Flexibility
Compose and decompose multi-digit numbers with decimals to the thousandths in multiple ways using the values of the digits in each place. Demonstrate the compositions or decompositions using objects, drawings and expressions or equations.
I understand that multi-digit numbers can be pulled apart and put back together again in a variety of ways through a variety of methods.
- Find three ways to decompose the number 4,321.43 in word form.
- If you had five hundreds, twenty tens, and no ones, what number would you have?
- Compose a number with at least seven millions and twenty four thousands.
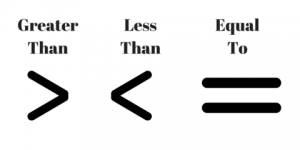 MA.5.NSO.1.4 – Place Value Comparisons
MA.5.NSO.1.4 – Place Value Comparisons
Plot, order and compare multi-digit numbers with decimals up to the thousandths.
I can explain the difference between two multi-digit numbers from as high as the millions place to as low as the thousandths place and even put them in order from least to greatest.
- Given the numbers 8,413.52 and 8,413.05, which is greater and why?
- Write the following numbers in order from least to greatest: 524.77, 500.77, 523.76, 524.8
- Compare the numbers 0.42 and 0.420 using less than, greater than, or equal to symbols.
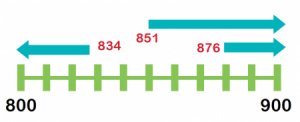 MA.5.NSO.1.5 – Place Value Rounding
MA.5.NSO.1.5 – Place Value Rounding
Round multi-digit numbers with decimals to the thousandths to the nearest hundredth, tenth or whole number.
I can look at multi-digit numbers as high as the millions place and as low as the thousandths place, then round those numbers as needed.
- Round 415.35 to the nearest tenth.
- Round the number above to the nearest ten.
- Round 4,153,504 to the nearest hundred thousand.
 MA.5.NSO.2.1 – Standard Multiplication
MA.5.NSO.2.1 – Standard Multiplication
Multiply multi-digit whole numbers including using a standard algorithm with procedural fluency.
I can multiply multi-digit whole numbers using the standard method, even if I have or know other methods for solving the problem.
- Multiply 562 by 2.
- Multiply 79 by 67.
- Multiply 65 by 94.
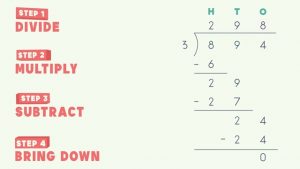 MA.5.NSO.2.2 – Standard Division
MA.5.NSO.2.2 – Standard Division
Divide multi-digit whole numbers, up to five digits by two digits, including using a standard algorithm with procedural fluency. Represent remainders as fractions.
I can divide multi-digit whole numbers using the standard method, or long division, and explain any remainder as numerator of a fraction.
- Divide 84 by 2.
- Divide 791 by 35.
- Divide 14,172 by 15.
 MA.5.NSO.2.3 – Adding and Subtracting Decimals
MA.5.NSO.2.3 – Adding and Subtracting Decimals
Add and subtract multi-digit numbers with decimals to the thousandths, including using a standard algorithm with procedural fluency.
I can add and subtract multi-digit numbers with decimals to find the correct sum or the correct difference.
- Add 42.14 to 53.99.
- Subtract 73.2 from 84.6.
- Subtract 412.1 from 1,788.23.
 MA.5.NSO.2.4 – Multiplying and Dividing Rounded Decimals
MA.5.NSO.2.4 – Multiplying and Dividing Rounded Decimals
Explore the multiplication and division of multi-digit numbers with decimals to the hundredths using estimation, rounding and place value.
I can round multi-digit whole numbers with decimals to the thousandths, then multiply and divide those numbers to determine the reasonableness of a product or a quotient.
- Estimate the product of 6.43 times 9.
- Estimate the quotient of 643 divided by 9.
- Estimate the quotient of 7,842 divided by 100.
 MA.5.NSO.2.5 – Multiply and Dividing Decimals
MA.5.NSO.2.5 – Multiply and Dividing Decimals
Multiply and divide a multi-digit number with decimals to the tenths by one tenth and one-hundredth with procedural reliability.
I can multiply and divide multi-digit numbers with decimals to find the correct product or the correct quotient.
- Multiply 42.14 by 53.9.
- Divide 42.14 by 5.
- Divide 5,237.5 by 25.
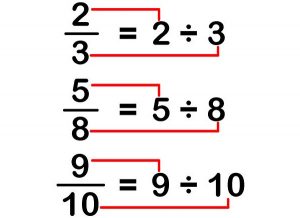 MA.5.FR.1.1 – Fractions as Division
MA.5.FR.1.1 – Fractions as Division
Given a mathematical or real-world problem, represent the division of two whole numbers as a fraction.
I understand that a fractional line between the numerator and the denominator symbolizes division and can be used to express whole numbers in a problem.
- What is the meaning of 5/10?
- In a forest of 300 trees, 100 of them will be cut down. Express that statement as a fraction.
- The library is giving away 54 of its 840 books to save room for new books. Use a fraction to represent that figure.
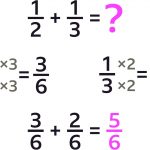 MA.5.FR.2.1 – Adding and Subtracting Fractions
MA.5.FR.2.1 – Adding and Subtracting Fractions
Add and subtract fractions with unlike denominators, including mixed numbers and fractions greater than 1, with procedural reliability.
I can add and subtract fractions with different denominators, then simplify my solutions.
- Add 4/5 to 1/5, then write your .
- Subtract 1/12 from 3/24.
- Subtract 5/6 from 8/9.
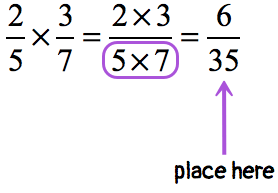 MA.5.FR.2.2 – Multiplying Fractions
MA.5.FR.2.2 – Multiplying Fractions
Extend previous understanding of multiplication to multiply a fraction by a fraction, including mixed numbers and fractions greater than 1, with procedural reliability
I can multiply fractions, including mixed numbers that I can turn into fractions, then simplify my solutions.
- Multiply 2/5 and 5/8, then write your answer in simplest form.
- Multiply 3/10 and 5/9, then write your answer in simplest form.
- Multiply 5 1/2 and 3, then write your answer in simplest form.
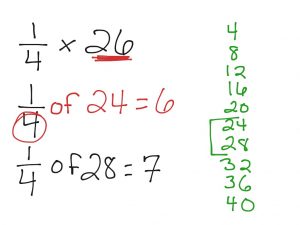 MA.5.FR.2.3 – Predicting Products for Fractions
MA.5.FR.2.3 – Predicting Products for Fractions
When multiplying a given number by a fraction less than 1 or a fraction greater than 1, predict and explain the relative size of the product to the given number without calculating.
I can predict or estimate what will happen to a whole number if I multiply it by a fraction less than 1 or a fraction greater than 1.
- If you multiply 16 by 1/2, will the product be greater than 16 or lower?
- In the operation of 145 times 14/15, will the product be closer to 145 or 0?
- When multiplying 30 by 4/10, will the product be closer to 30 or 0?
 MA.5.FR.2.4 – Dividing Fractions
MA.5.FR.2.4 – Dividing Fractions
Extend previous understanding of division to explore the division of a unit fraction by a whole number and a whole number by a unit fraction.
I can divide fractions by whole numbers and whole numbers by fractions, using reciprocals, then simplify my solutions.
- Divide 9/11 by 3.
- Divide 3/7 by 2.
- Divide 12 by 3/4.
 MA.5.AR.1.1 – Multi-Step Problems
MA.5.AR.1.1 – Multi-Step Problems
Solve multi-step real-world problems involving any combination of the four operations with whole numbers, including problems in which remainders must be interpreted within the context.
I understand that many real-world problems involve multiple steps and I can use whatever combination of the four operations is required to find a correct solution.
- Alisha fills a one gallon jug with 4/5 of water. She then pours 1/4 of that water into a pitcher and the rest of it equally into 6 glasses. How much water is in each glass?
- David works 4 3/4 hours of each weekday working at his father’s Italian restaurant. If he is paid $9 per hour, how much does he make in two weeks?
- A grocery store has 53 boxes of raspberries. Each box contains 42 raspberries. The raspberries were repackaged into smaller bags of 14 raspberries. How many bags of raspberries were made?
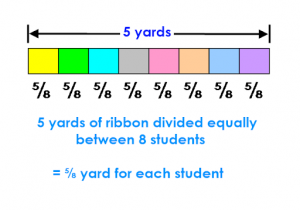 MA.5.AR.1.2 – Real World Problems with Fractions
MA.5.AR.1.2 – Real World Problems with Fractions
Solve real-world problems involving the addition, subtraction or multiplication of fractions, including mixed numbers and fractions greater than 1.
I can accurately solve real-world problems that include fractions, including mixed numbers and fractions greater than 1.
- Natasha spent 1/4 of her paycheck on Monday. She also spent 2/5 of it on Tuesday. What fraction of her paycheck does she have left?
- A baker uses 2 5/9 pounds of flour to make cookies for his bakery. He uses 5/6 more pounds of flour than the second baker down the street. How many pounds of flour is the second baker using?
- Helen bought 36 pencils and shared them equally with four of her friends. If three of her friends gave their pencils away to other classmates, how many pencils does the fourth friend still have?
 MA.5.AR.1.3 – Real-World Fraction Division
MA.5.AR.1.3 – Real-World Fraction Division
Solve real-world problems involving division of a unit fraction by a whole number and a whole number by a unit fraction.
I can recognize when a world problem is asking me to divide fractions and whole numbers, then solve and simplify.
- A building has a total of 42 3/4 rooms and needs to be split evenly among 3 groups. How many rooms will each group get?
- A library has 650 books. The main librarian needs to give away 1/4 of those books. How many books will be left?
- If Kelly has 3 pizzas and has to split them up evenly among herself and 5 other friends, how many pieces can each person have, including Kelly?
Translate written real-world and mathematical descriptions into numerical expressions and numerical expressions into written mathematical descriptions
TBD
- TBD
- TBD
- TBD
Evaluate multi-step numerical expressions using order of operations.
TBD
- TBD
- TBD
- TBD
Determine and explain whether an equation involving any of the four operations is true or false.
TBD
- TBD
- TBD
- TBD
Given a mathematical or real-world context, write an equation involving any of the four operations to determine the unknown whole number with the unknown in any position.
TBD
- TBD
- TBD
- TBD
Given a numerical pattern, identify and write a rule that can describe the pattern as an expression.
TBD
- TBD
- TBD
- TBD
Given a rule for a numerical pattern, use a two-column table to record the inputs and outputs.
TBD
- TBD
- TBD
- TBD
Solve multi-step real-world problems that involve converting measurement units to equivalent measurements within a single system of measurement.
TBD
- TBD
- TBD
- TBD
Solve multi-step real-world problems involving money using decimal notation.
TBD
- TBD
- TBD
- TBD
Classify triangles or quadrilaterals into different categories based on shared defining attributes. Explain why a triangle or quadrilateral would or would not belong to a category.
TBD
- TBD
- TBD
- TBD
Identify and classify three-dimensional figures into categories based on their defining attributes. Figures are limited to right pyramids, right prisms, right circular cylinders, right circular cones and spheres.
TBD
- TBD
- TBD
- TBD
Find the perimeter and area of a rectangle with fractional or decimal side lengths using visual models and formulas.
TBD
- TBD
- TBD
- TBD
Explore volume as an attribute of three-dimensional figures by packing them with unit cubes without gaps. Find the volume of a right rectangular prism with whole-number side lengths by counting unit cubes.
TBD
- TBD
- TBD
- TBD
Find the volume of a right rectangular prism with whole-number side lengths using a visual model and a formula.
TBD
- TBD
- TBD
- TBD
Solve real-world problems involving the volume of right rectangular prisms, including problems with an unknown edge length, with whole-number edge lengths using a visual model or a formula. Write an equation with a variable for the unknown to represent the problem.
TBD
- TBD
- TBD
- TBD
Identify the origin and axes in the coordinate system. Plot and label ordered pairs in the first quadrant of the coordinate plane.
TBD
- TBD
- TBD
- TBD
Represent mathematical and real-world problems by plotting points in the first quadrant of the coordinate plane and interpret coordinate values of points in the context of the situation.
TBD
- TBD
- TBD
- TBD
Collect and represent numerical data, including fractional and decimal values, using tables, line graphs or line plots.
TBD
- TBD
- TBD
- TBD
Interpret numerical data, with whole-number values, represented with tables or line plots by determining the mean, mode, median or range.
TBD
- TBD
- TBD
- TBD